Numerous theorems, such as those in geometry, are often presented in multimodal forms (e.g., diagrams). Humans benefit from visual reasoning in such settings, using diagrams to gain intuition and guide the proof process. Modern Multimodal Large Language Models (MLLMs) have demonstrated remarkable capabilities in solving a wide range of mathematical problems. However, the potential of MLLMs as Automated Theorem Provers (ATPs), specifically in the multimodal domain, remains underexplored. In this paper, we introduce the Multimodal Automated Theorem Proving Benchmark (MATP-Bench), a new Multimodal, Multi-level, and Multi-language benchmark designed to evaluate MLLMs in this role as multimodal automated theorem provers. MATP-BENCH consists of 1056 multimodal theorems drawn from high school, university, and competition-level mathematics. All these multimodal problems are accompanied by formalizations in Lean 4, Coq and Isabelle, thus making the benchmark compatible with a wide range of theorem-proving frameworks. MATP-BENCH requires models to integrate sophisticated visual understanding with mastery of a broad spectrum of mathematical knowledge and rigorous symbolic reasoning to generate formal proofs. We use MATP-BENCH to evaluate a variety of advanced multimodal language models. Existing methods can only solve a limited number of the MATP-BENCH problems, indicating that this benchmark poses an open challenge for research on automated theorem proving.
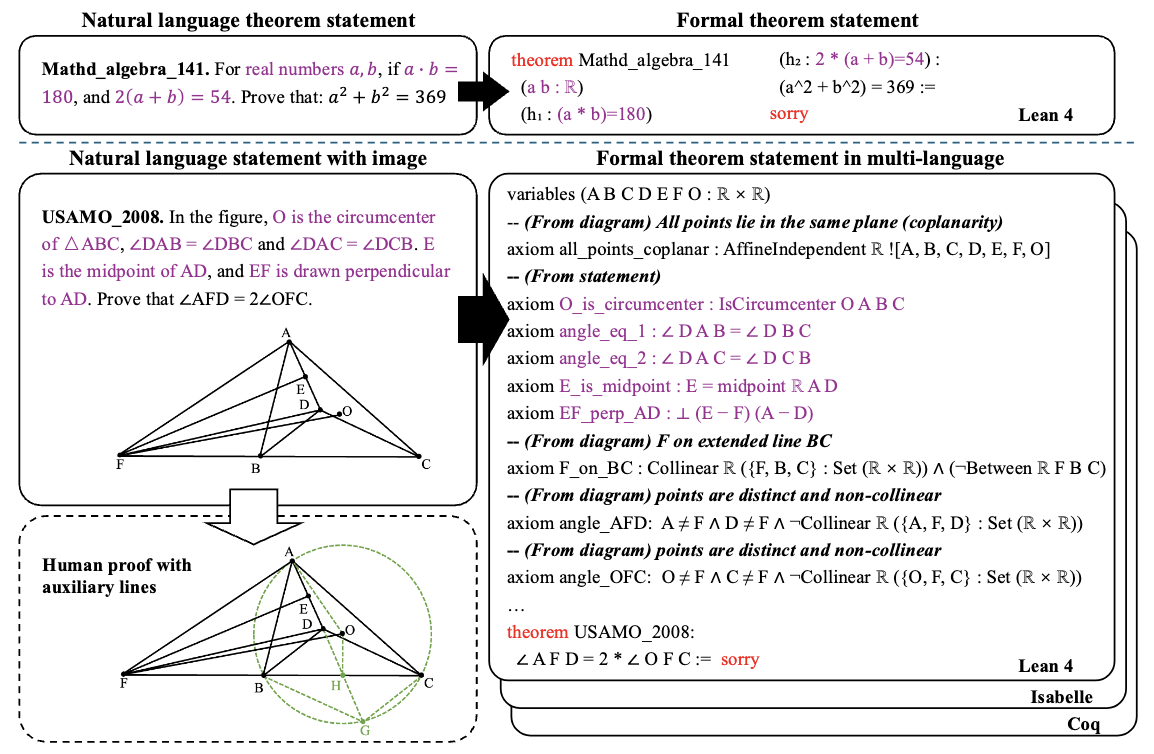
Multimodal theorems consist of an image paired with a natural language theorem statement, which complement each other to convey complete theorem information. Furthermore, additional auxiliary constructions are often essential for their proof (as shown in the bottom left subfigure). In traditional ATP, theorem formalization relies solely on textual statements (we use purple to indicate premises derived from the original statement), whereas MATP requires the model to extract critical premises not explicitly expressed in the text by analyzing accompanying diagrams (see From diagram on the right). We provide formalized versions of all multimodal theorems in Lean4, Coq, and Isabelle.
Automated Theorem Proving (ATP): In this task, the system takes a formalized theorem statement T as input. The goal is to generate a formal proof P such that:
Here, Check denotes the built-in proof verifier of the formal system (such as Lean, Coq, or Isabelle), which ensures that the generated proof P is a valid derivation of theorem T.
Multimodal Automated Theorem Proving (MATP): In this task, the input to the MATP system is a pair (I, S), where:
As shown in Figure 1, the natural language statement S and the information from the multimodal input I are complementary, together forming a complete theorem. Hence, the model must first generate the complete formal theorem T, then generate a valid formal proof P. The entire MATP task can be summarized as:
To avoid modality leakage, where the model could ignore visual inputs, we provide only natural language S and image I, without the formalized theorem T. This encourages the model to interpret and reason over multimodal inputs, as humans do when proving multimodal theorems. Furthermore, we incorporate a theorem verification task in the experimental setup to ensure that the formal theorems automatically generated by the multimodal model are consistent with the problem statement, rather than fabricating simple theorems arbitrarily.
We provide a detailed comparison between existing variable math reasoning benchmarks and MATP-Bench.

MATP-BENCH introduces concrete multimodal contexts to jointly evaluate models on visual understanding, mathematical reasoning, and symbolic manipulation. As shown in the lower part of Figure 1, each theorem consists of an image and a corresponding natural language description, which complement each other to form a complete statement. MATP-BENCH provides formalizations of these multimodal theorems in Lean 4, Isabelle, and Coq. To the best of our knowledge, MATP-BENCH is the first multimodal automated theorem proving benchmark covering all three of these languages.
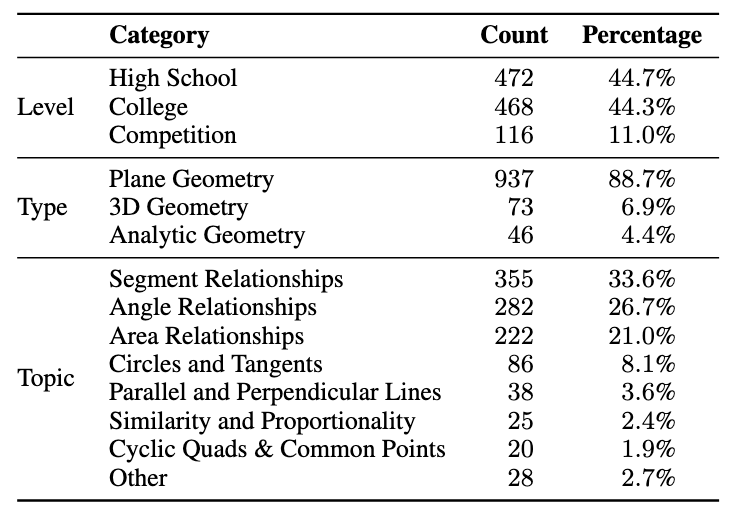
The problems in MATP-BENCH span three distinct educational stages—high school, university, and competitions—systematically covering a wide range of difficulty levels from elementary to advanced. Specifically, the high school and university problems are collected from publicly available multimodal math problem datasets, while the competition problems are sourced from public Mathematical Olympiad examinations. Moreover, the multimodal theorems in MATP-BENCH are primarily centered around the domain of geometry, spanning plane geometry, 3D geometry, analytic geometry.
We aim to achieve end-to-end multimodal automated theorem proving (Task 1), where the input is a natural language theorem and an image, and the output is a formal theorem and its proof, i.e. ProverMATP(I, S) → (T, P). Furthermore, to prevent the model from generating formal theorems that do not align with original problems, we separately set up multimodal theorem formalization (Task 2) for verification, which aligns with LeanEuclid. Thus, we divide the task into two progressively challenging sub-tasks:
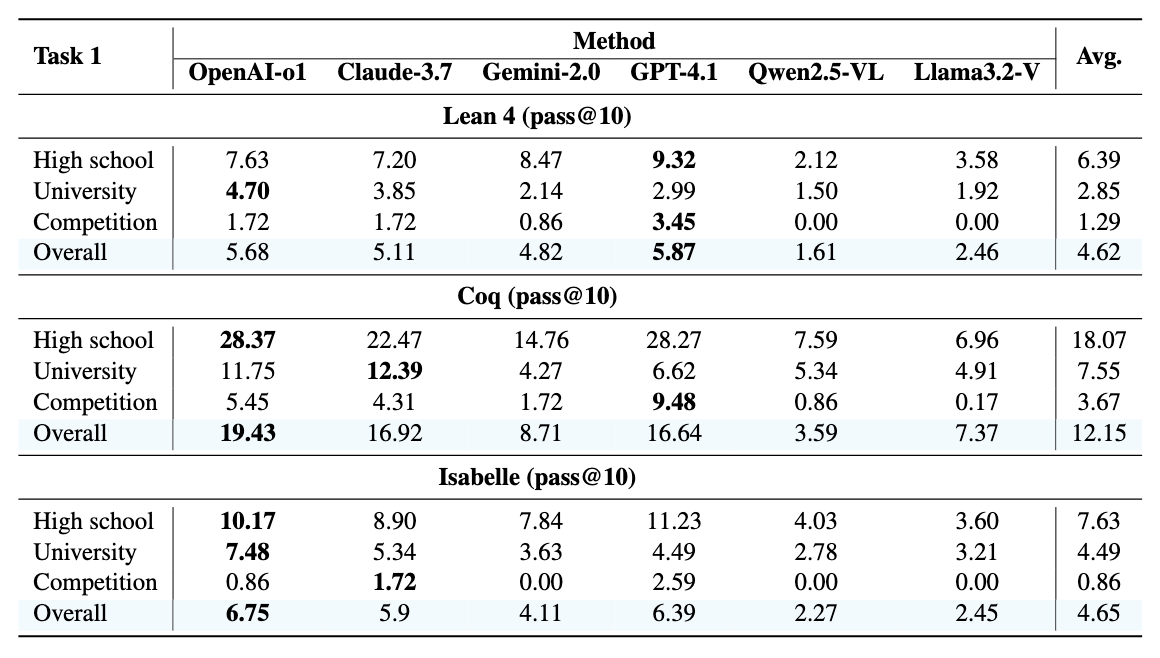
Experimental results of Multimodal Automated Theorem Proving (Task 1), which requires model to generate both formalized theorem and proof. We adopt pass@10 as the evaluation metric. We further present the experimental results of pass@n (n=1, n=5) in our paper (Appendix).
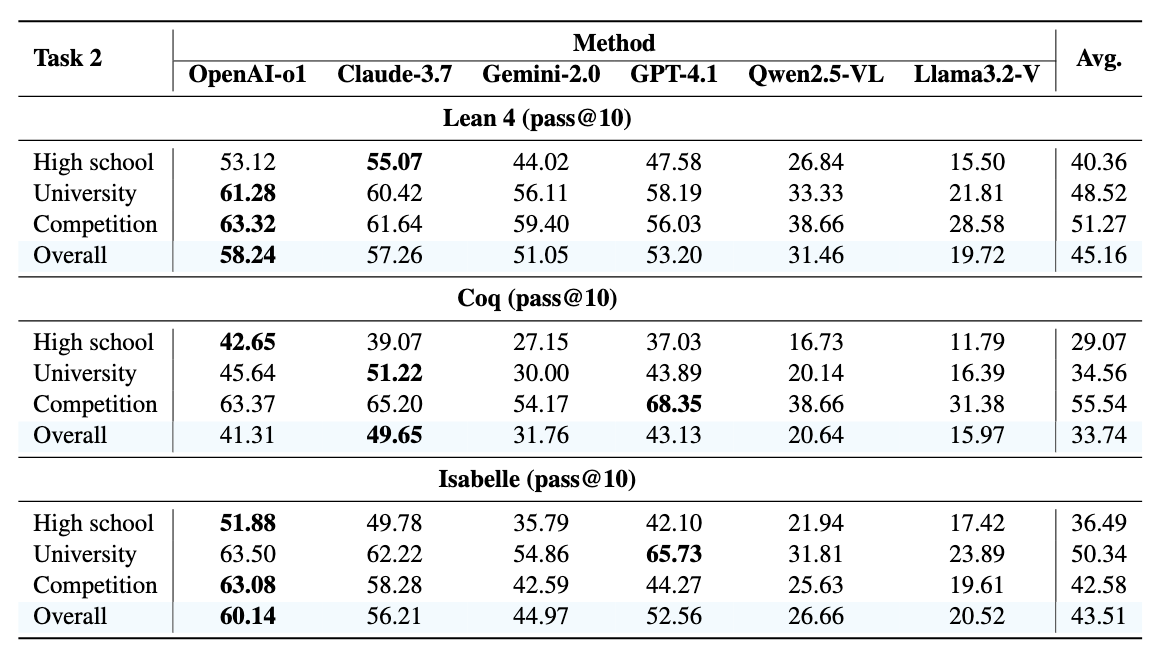
Experimental results of Multimodal Theorem Formalization (Task 2), which only require model to generate formalized theorem. We use GPT-4o as the judge and adopt pass@10 as the evaluation metric. We present the experimental results of pass@n (n=1, n=5) in our paper (Appendix).
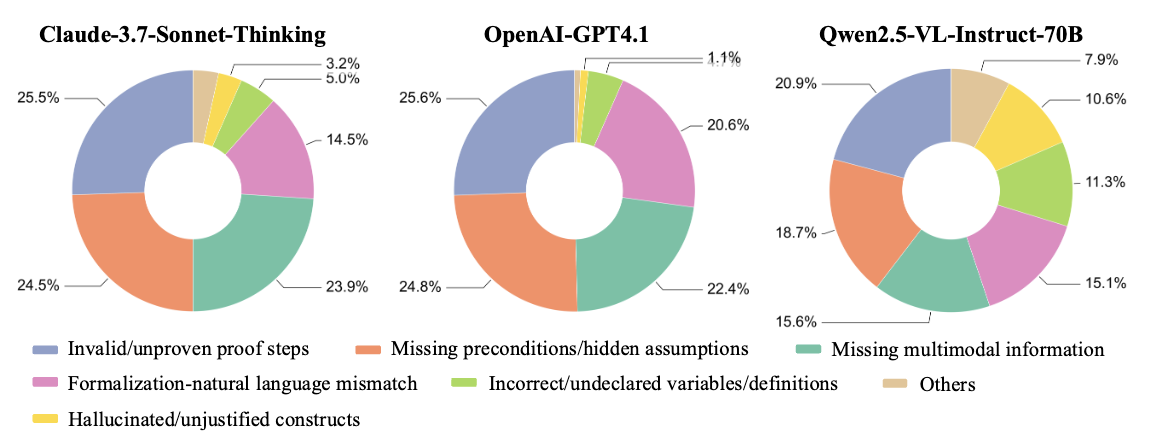
We analyze the types of errors generated by multimodal models in theorem proving. As shown in Figure, the results indicate that different models exhibit both common errors and specific issues. This results of Claude and GPT-4.1 suggest that even for relatively better-performing models, the core challenges lie in complex logical reasoning and identifying and utilizing all implicit and explicit information required by the theorem. More fundamental formalization errors such as missing/incorrect library imports and incorrect/undeclared variables/definitions are more prominent in Qwen2.5. This might indicate that while Qwen struggles with proof step errors, it also faces significant issues in generating basic code that conforms to the formal language specification. Overall, all models exhibit problems with incomplete information understanding and broken reasoning chains.
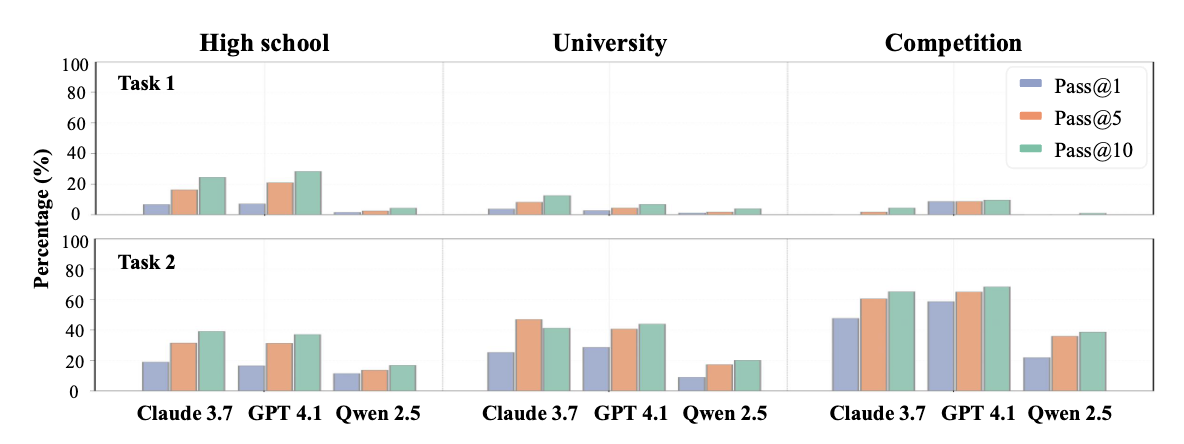
the analysis of the pass@n performance of multimodal models in the Coq language shows that for both complete theorem formalization and proof generation (Task 1) and formalization only (Task 2), allowing models to generate more candidates (from pass@1 to pass@10) generally increases the success rate. However, the pass@n success rate for Task 1 is significantly lower than the pass@n success rate for Task 2 across all difficulty levels and models. This large performance gap between Task 1 and Task 2 is consistent across all pass@n settings, demonstrating that models have shown a certain ability in converting natural language descriptions and geometric figures into Coq formal statements (Task 2 pass@n is relatively high), but still face significant challenges in the subsequent complex logical reasoning and constructing formal proofs.
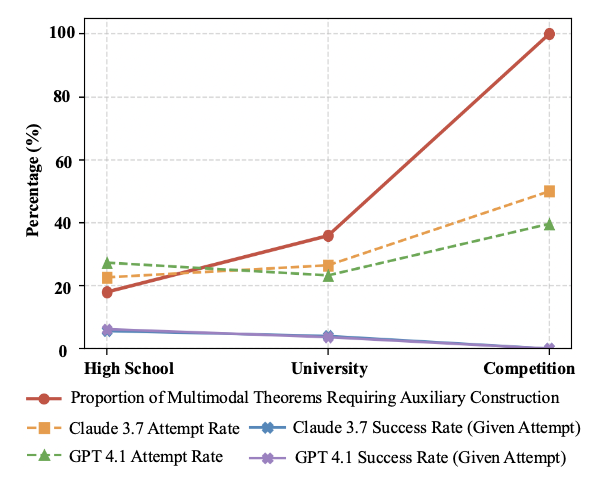
A characteristic distinguishing multimodal theorem proving from pure text theorem proving is that many theorems require the construction of auxiliary lines to aid thinking, especially problems at the competition level. Therefore, we further investigate the models' ability to construct auxiliary lines during the proof process. With the increase in theorem difficulty, the proportion of problems requiring auxiliary construction significantly rises, confirming the importance of auxiliary construction for solving high-difficulty geometric theorems. Claude 3.7 and GPT 4.1, which perform best in Task 1 and Task 2, attempt to perform auxiliary constructions when generating proofs, and this attempt rate also increases with difficulty, which indicates that the models possess a certain degree of autonomous auxiliary construction capability and awareness. However, the success rate of these proofs containing auxiliary constructions is very low. This prominently indicates that while models can introduce steps or concepts involving auxiliary constructions in proofs, they cannot effectively utilize these constructions to advance the proof process.
@misc{he2025matpbenchmllmgoodautomated,
title={MATP-BENCH: Can MLLM Be a Good Automated Theorem Prover for Multimodal Problems?},
author={Zhitao He and Zongwei Lyu and Dazhong Chen and Dadi Guo and Yi R. Fung},
year={2025},
eprint={2506.06034},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2506.06034},
}